Today I want to talk about model slicing which is one of the more advanced features of Spec Explorer. Slicing is extremely powerful, because it allows you to build your models very generically, and then create many slices of that model with differing purposes.
I’m going to show some very simple examples on how slicing works, and then I will dig up the Binary Search Tree model to illustrate how this would work in practice.
Slicing
For my example on slicing I’m going to construct a very simple model. The state is one integer variable, and I have two rules defined the following way:
[Rule(Action = "A()")]
static void A()
{
value *= -1;
}
[Rule(Action = "B()")]
static void B()
{
value++;
}
Rule “A” flips the sign of the value and “B” increases it by one. The state space of this model is infinite. If you explore it you get something like:
Let’s look at what we can do using slicing. In general slicing works like this:
machine Scenario() : Main where ForExploration = true
{
(A | B)
}
machine SlicedAccumulatorModelProgram() : Main where ForExploration = true
{
Scenario || AccumulatorModelProgram
}
You define a “scenario” and then you interleave it with your model program. The above scenario (A | B) will do either A or B, but only one of them:
We can also use slicing to fix a sequence of rules. Say we would like to first execute A then followed by B, we can do that using:
machine Scenario() : Main where ForExploration = true
{
(A ; B)
}
We can combine sequences by concatenating them:
machine Scenario() : Main where ForExploration = true
{
(A | B) ; (A ; B)
}
We can repeat a scenario:
machine Scenario() : Main where ForExploration = true
{
B*
}
Repeating B is itself an infinite model because it simply grows the counter.
Interestingly we could also repeat A but this just yields:
Because flipping the sign on zero has no effect.
We can do B followed by A repeatedly instead:
machine Scenario() : Main where ForExploration = true
{
B ; A*
}
Now A has an effect, but it repeats over two values (-1 and 1) so the sliced model is finite.
Interestingly we can construct other repeated scenarios that also results in a finite model:
machine Scenario() : Main where ForExploration = true
{
(A; B)*
}
When repeating A followed by B this causes the combined action to alternate between increasing and decreasing the value.
This is just some of the very basic things that we can do using slicing. I will stop the example here and continue on to a real example.
Slicing applied to a binary search tree
Enough with the toy examples, let’s try this on the BST case. If you go back and read up on the BST model you will find that one of the conclusions we drew back then was that for MBT to generate a model that would provide us with 100% code coverage of the BST implementation we were forced to model trees of size 4, quoting:
“For this special case the node being deleted must have both a left and right sibling and in addition the right sibling must also have a left sibling […] it is simply not possible for the model to construct such a tree because it is limited to using 3 nodes. To cover this scenario, we would need to extend the model parameter ranges to Add and Remove from 0..2 to 0..3. […] Were you to generate the tests, you would end up with 193 test cases.”
The statement is still true; we need four nodes in the tree. But a generic 4-node model has shown to be overkill. Instead what we can do is fix the values of the two first nodes and then continue with the generic model from thereon. I will show you how we obtain this.
First we split the input range into two ranges, one which we use in our slicing (fixing parameters) and one that we let Spec Explorer choose parameters from:
config ParameterCombination: Main
{
action abstract static bool BSTTest.Add(int x)
where x in {0..1};
action abstract static bool BSTTest.Remove(int x)
where x in {-1,0..1};
}
config SlicedParameter: Main
{
action abstract static bool BSTTest.Add(int x)
where x in {-2..-1};
}
The slice will use x values -2 and -1, while the generic model will use 0 and 1. For the slice we do not intend to model the Remove method. You can very well also model Remove, it’s just not necessary. Keep in mind though if you were to model Remove generically on the inputs -2 to 1 then the model can Remove nodes -2 and -1 but it cannot re-add them.
Next we need to construct a model program for the sliced input parameter (-2 and -1). This is an exact copy of the generic model program just using a different input configuration:
machine SlicedModelProgram() : Main where ForExploration = false
{
construct model program from SlicedParameter
where scope = "Combinatorics.BSTModelProgram"
}
You can explore this model, but because we didn’t limit the input parameters to Remove, it will just explode (where you to implement the Remove method in the sliced configuration it would just be an exact duplicate of the model on 1 and 2).
The next step is to define the actual scenario we are interested in. To obtain the required base tree we need to add nodes -1 and -2 – in that order:
machine SlicedTreeScenario() : Main where ForExploration = true
{
Add(-1); Add(-2)
}
Too simple, right? You can explore this scenario:
Notice that this is just a static scenario – nothing is explored yet, thus some values are unknown.
Once we interleave this scenario with a model program, Spec Explorer will look for the sequence S0: Add(-1)/_ Add(-2)/_ in the model program and only include those branches that contains this sequence. The underscores are wildcards, that can take any value. In this case Spec Explorer will accept Add(-1)/True or Add(-1)/False. If you omit a parameter (or return value) it is treated as an underscore. You can also specify directly the required output to be True in our case, but it does not matter because the sequence Add(-1); Add(-2) will always return True for both rules. Where you instead to construct the scenario: Add; Add/False, then you tell Spec Explorer that the second Add call must return False which only happens in the cases where the same value was added twice (e.g. Add(-1)/True; Add(-1)/False). Hopefully this makes sense.
Now we interleave this scenario with our slicing model program to generate the sliced model:
machine SlicedTreeModelProgram() : Main where ForExploration = true
{
SlicedTreeScenario || SlicedModelProgram
}
And we can also explore this model:
Now that we have interleaved the actual model we get actual model exploration, which we can see by the fact that the states contain data. Now the exploration was fixed because we told it just to follow one scenario, but we are free to do more with this sliced model:
machine JoinedBSTModelProgram() : Main where ForExploration = true
{
SlicedTreeModelProgram ; BSTModelProgram
}
This joined model program starts out by exploring our sliced model program and then carries on exploring the generic model:
From the exploration graph it is evident that all states start out with the -1,-2 sequence, which is exactly what we wanted. The tree structure we wanted to build from the original description conforms with the tree built in state (-1,-2,1,0).
Because we fixed the input sequence to start with Add(-1); Add(-2) we obtain 4-node trees with the right construct with only 12 states, and generating tests from this model results in just 16 additional test cases instead of the 160 tests we got in addition when going to a 4-noded generic model.
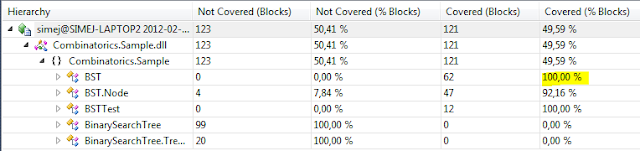
Generating and executing the tests from the two models results in 100% code coverage of the BST class:
Conclusion
Model slicing is a powerful feature of Spec Explorer which allows you to generate additional models that are sliced subsets of a bigger model. This is very useful in cases where we are interested in the behavior of the system under some special circumstances – like the binary search tree example.
Using model slicing you can also model your system without any limitation, creating infinite state space models. Then this infinite model can be sliced into many finite models later. This allows you to think more about the system you are modeling and less about how to avoid the state space blowing up. Furthermore, you can use slicing as a means to look into your infinite model and see if it behaves correctly in a constraints environment. This can help you spot inconsistencies in your infinite models. Once you are happy with your infinite model you can let Spec Explorer go nuts on it using On-The-Fly testing.
You can also dictate exact scenarios if you are interested in some specific scenario. So in our BST case we could just have written:
machine Test() : Main where ForExploration = true
{
((Add(-1) ; Add(-2) ; Add(1) ; Add(0) ; Remove(-1)) || UnparameterizedBSTModelProgram)
}
To construct the exact scenario we were looking for. Although this has little to do with modeling, and we could just as well write a unit test to do that.










Hello,
ReplyDeleteCan you send me a mail to contact with a reponsable of MBT tool Spec Xplorer please? We are really interested in this tool in my company. My mail is: icuevascanals@lear.com
Hello Simon,
ReplyDeleteI am a software test engineer for automotive applications in a multinational company. We are really interested in the Microsoft tool Spec Xplorer and start using MBT for our test. We don´t find a contact person which can give us a presentation of that tool and explain us if we need a new license or just with Visual Studio license will be ok. Could you give to one responsable of that tool my professional mail Icuevascanals@lear.es and ask him to contact with me. Thanks a lot!!